Archives

1. What is the Perimeter of a Rectangle? The perimeter of a rectangle is the total distance around its outer boundary — the sum of all four sides. If you imagine walking along every edge…

1. What is the Area of a Triangle? The area of a triangle is the total region enclosed by its three sides, measured in square units. In other words, it is the amount of two-dimensional…

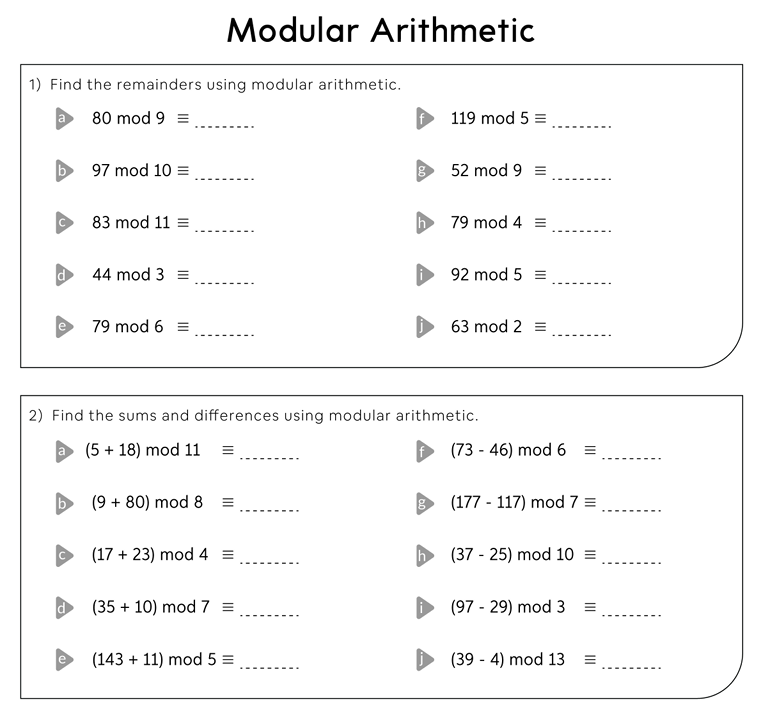
Modular arithmetic is an important concept in number theory and algebra, often described as "clock arithmetic," where numbers wrap around after reaching a certain value called the modulus. For integers $a$ and $b$ with modulus…

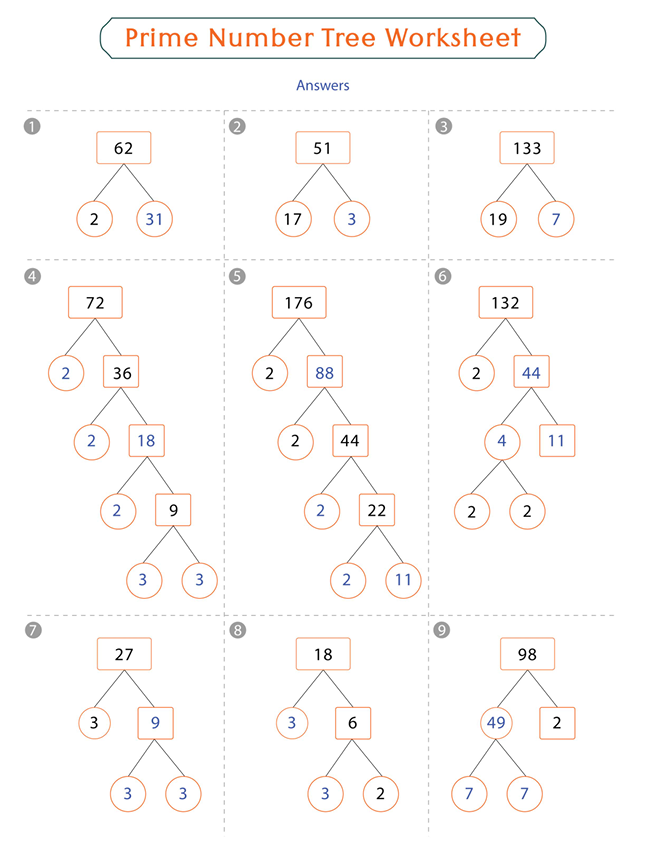
Prime numbers are the building blocks of all natural numbers, as every number greater than 1 can be expressed as a product of prime numbers. A prime number is defined as a number greater than…

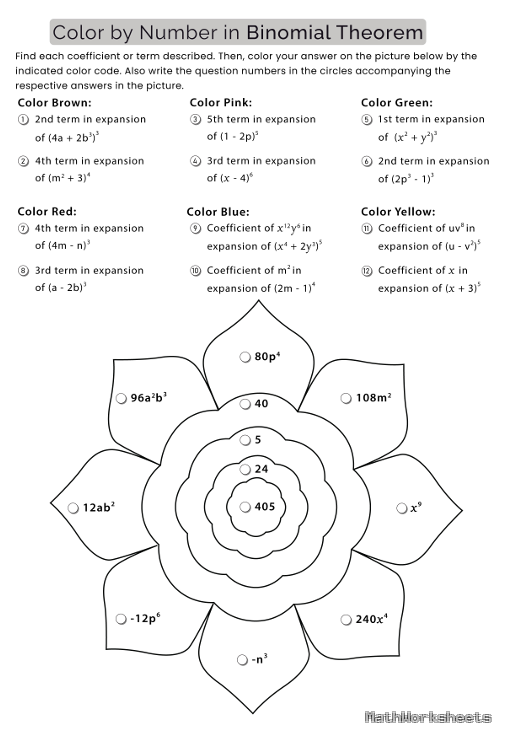
The Binomial Theorem is a powerful tool in Algebra for expanding expressions of the form $ (a + b)^n $. It states that:  ${(a + b)^n} = \sum\limits_{k = 0}^n {\left( \begin{array}{c} n\\ k \end{array}…

Complex numbers are a fundamental concept in Algebra and higher-level mathematics, extending the idea of real numbers to include solutions to equations like $x^2 + 1 = 0$. A complex number is written in the…

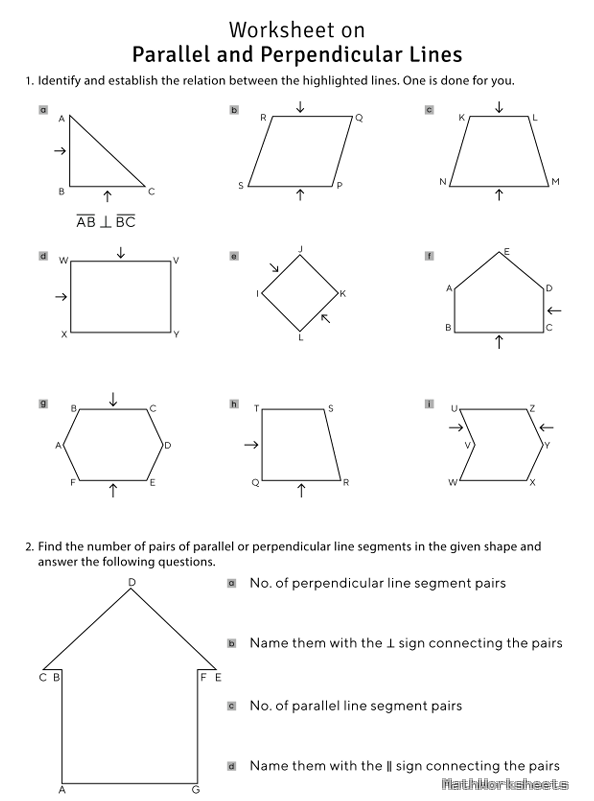
Understanding parallel and perpendicular lines is a fundamental concept in Geometry, essential for analyzing angles, slopes, and coordinate plane relationships. Two lines are parallel if they have the same slope: $ m_1 = m_2 $and…

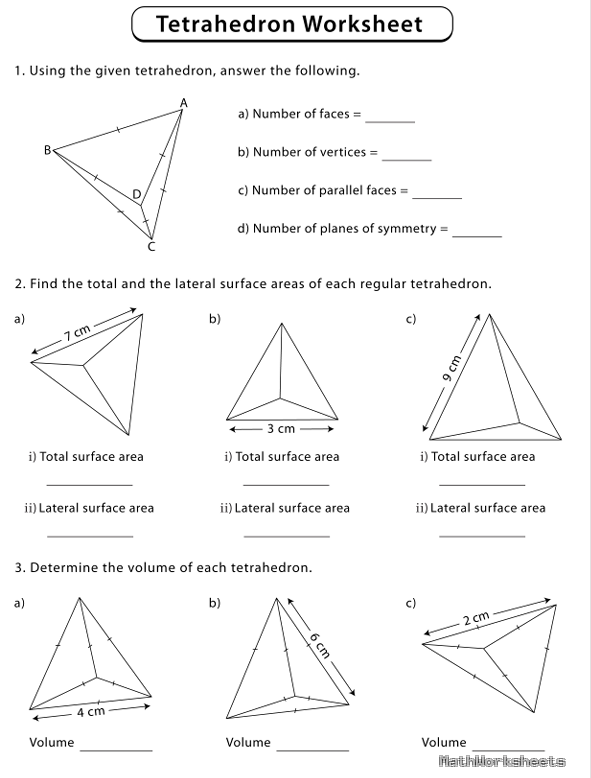
Understanding the geometry of a tetrahedron is a key part of learning about three-dimensional shapes. A tetrahedron is a polyhedron with four triangular faces, and its volume and surface area can be calculated using the…

Calculating the percent of a number is an essential math skill with applications in everyday life, from shopping discounts to data analysis. The basic formula for finding a percent of a number is:$ \text{Percent of…